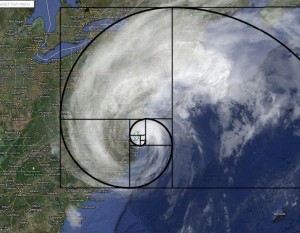
デザインを勉強すると必ず一度は耳にする黄金比という言葉。これは人が最も美しいと感じる比率で、トランプや名刺、ミロのビーナスなどの芸術作品、パルテノン神殿などの建造物など、様々な場所に散りばめられている。
特徴のひとつとして黄金比の長方形から正方形を抜き出すと、残った長方形も黄金比になる。
黄金比とフィボナッチ
その比率は 1 : 1.618…で、円周率のように永遠に数が続いていく無理数だ。いったい誰が決めたんだという感じ。古代ギリシャ人は感覚的に美しいと感じたのだろうか?
実はこの黄金比は自然の中にも散りばめられており、人が勝手に美しいと感じている訳ではなく、自然の法則だったということがフィボナッチ数列との関係で分かる。
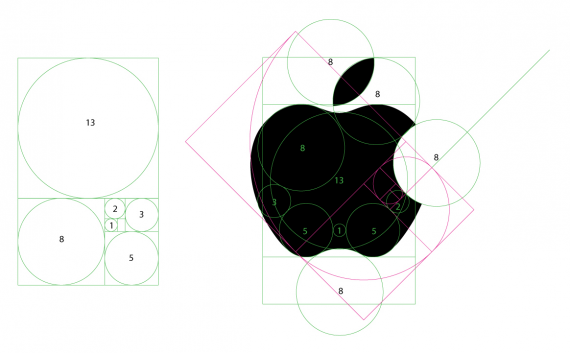
美しいと感じる形には至る所に黄金比が隠れている
ミロのビーナスは紀元前130年頃に作られ、フィボナッチは1170年頃に生誕なので、およそ1300年後に発見されたフィボナッチ数列とは、すごく単純な数字の並びで、
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144
のように増えていく。前の2つを足した数が次の数。みたいな法則。
一見すると、これが黄金比と関係あるのか?と思うんだけど、実はすでに黄金比が見え隠れしていて、隣接する2つの数字を右から左で割ると黄金比に近づいていく。例えば13÷8=1.625で既に黄金比にかなり近い。この調子で限りなく黄金比に近くなる。計算式としては(1+√5)÷2となる。
自然界に隠れる黄金比
不思議なことに、フィボナッチ数列の中には黄金比が隠れていたわけだけど、黄金比を角度に適応した黄金角というのもある。360°を 1 : (1+√5)÷2に分けた約137.5°がそうだ。
フィボナッチ数列という数字の並びから、黄金比1 : 1.618と黄金角137.5°が見つかった所で予備知識は終わり。ようやく本題の動画へ。それらの数字がどのように自然界に登場するかを直感的にまとめた映像を紹介します。
自然界のデザインは進化における合理性の結晶なので、黄金比を美しいと感じる人の感性の裏には、極めて合理的な進化への美意識が隠されていたのだ。
